Après un long silence (un long silence plein d’autres projets), je lance enfin dans la publication des épisodes de la première saison d’Artborescience. La saison 1 n’étant plus disponible sur Radio Campus (car elle ne garde les podcasts que deux ans), les épisodes sont mis en ligne sur mon espacer et disponibles au téléchargement direct, ICI :

Artborescience S1 ep1, la théorie du chaos.

Bonne écoute, bonne lecture !

Artborescience, c’est l’émission sur Radio Campus qui élargit votre horizon des événements, c’est l’émission qui entrelace les découvertes de la science contemporaine et les trouvailles de la culture populaire, l’émission ouverte à toutes les formes d’arts et de poésie. Artborescience, c’est l’émission qui révèle des liens, c’est l’émission qui synthétise et qui alchimise, l’émission qui butine et qui fertilise, et enfin l’émission qui assume de tirer parfois les sciences par les cheveux.

Aujourd’hui : la théorie du chaos !

Intro : Extrait de Jurassic Park : « Qu’est-ce que c’est, cette théorie du chaos… Qu’est-ce que ça signifie ?…

La paléobotaniste incarnée par Laura Dern, dans cet extrait du film Jurassic Park de Steven Spielberg, feint certainement d’ignorer ce qu’est la théorie du chaos afin de bénéficier de la démonstration tactile de Jeff Goldblum. L’explication très condensée de ce séducteur de Ian Malcolm nous suggère que le chaos au sens physique n’est pas simplement synonyme de désordre comme il l’est dans le langage courant. Le chaos s’apparente-t-il au désordre, à l’ordre, ou bien aux deux ? Cette question (à laquelle nous répondrons en fait assez rapidement) nous permettra de parcourir les fascinantes facettes de cette théorie.

Nous allons couler avec cette goutte d’eau, qui glisse sensuellement sur la main du Dr Sattler, pour traverser les nuages et cerner le champ sémantique du chaos. Nous nous interrogerons sur son rôle dans l’apparition de la vie, ce qui nous amènera à opposer entropie et complexité et à entrevoir différents destins possibles pour notre Univers. Enfin, après avoir rebondi sur la surface fractale d’un chou romanesco, nous déboucherons sur une manière singulière de concevoir le monde et d’apprécier sa beauté.

Origines et définitions : chaos, sensibilité aux conditions initiales, effet papillon…

La théorie du chaos constitue l’une des trois grandes théories – l’une des trois grandes révolutions de la physique du XXe siècle – avec la physique quantique et la théorie de la relativité.
Dans les années 60′ et 70′, un intérêt pour les phénomènes irréguliers et instables émerge en plusieurs lieux, dans l’esprit de plusieurs scientifiques experts en divers domaines : des physiciens mais aussi des mathématiciens, des biologistes, des chimistes, des physiologues… Car le chaos est une théorie qui abat les frontières entre les disciplines.
Dans l’esprit de ces scientifiques, l’intérêt pour le chaos apparaît simultanément mais indépendamment, comme si l’idée flottait dans l’air du temps.

♪ tapis : UMN Mode, OST du jeu Xenosaga

L’un de ces scientifiques est Edward Lorenz. James Gleick, dans son ouvrage la théorie du Chaos, nous raconte son aventure chaotique.

En 1961, Edward Lorenz, météorologue, utilise l’informatique pour estimer les bulletins météo. Son ordinateur primitif lui permet de simuler les conditions atmosphériques, grâce à des formules simplifiées. Les résultats obtenus sont vraisemblables : ils correspondent en effet aux formes familières des mouvements d’air habituellement observés, avec un schéma familier de répétition. Pourtant, les répétitions obtenues ne sont jamais exactes, malgré leur forme familière. De plus, les formes nées du calcul semblent s’ordonner d’une manière particulière. Les cycles paraissent se répéter d’une façon reconnaissable, mais jamais tout à fait de la même façon. Ils sont similaires, mais jamais identiques.

Un jour d’hiver, Lorenz souhaite relancer l’observation d’une séquence, mais sur un temps plus long. Au lieu de redémarrer son programme du début, il choisit de le reprendre en cours de route. Quand il revient une heure après le lancement, après avoir bu son café, il constate quelque chose d’inattendu.

La nouvelle exécution aurait dû produire des résultats identiques à l’ancienne. Pourtant, les prévisions ont divergé très rapidement des précédentes, si bien que ces deux séquences issues d’une séquence unique finissent par ne plus rien avoir de commun… Cela alors même que, pourtant, Lorenz a bien pris soin de rentrer exactement les mêmes nombres que pour la première exécution. Les mêmes nombres, vraiment ? Eh non ! Lorenz se rend compte qu’il a arrondi ces nombres, en passant de nombres à six décimales pour la première séquence, de nombres à trois décimales pour la deuxième , en songeant que les dernières décimales ne pouvaient qu’avoir des conséquences aussi minuscules qu’elles-mêmes sur le résultat final. Or, ces décimales minuscules ont engendré des effets énormes. C’est ce fameux « effet papillon », qui exprime l’idée qu’une cause minuscule peut engendrer des effets démultipliés.

L’état final du système météorologique est donc imprévisible à terme ; certes, plus les paramètres d’entrée seront précis, meilleures seront les prévisions sur la durée ; mais il arrivera toujours un moment où ces prévisions finiront par ne plus ressembler du tout à la réalité après avoir divergé de plus en plus.

Nous pouvons ainsi définir le chaos : le chaos, tel que le conçoit le scientifique, ne signifie pas « absence d’ordre », nous verrons même qu’il s’agit bien du contraire – il ne signifie pas même « aléatoire » bien qu’il en ait l’apparence. Il signifie imprévisibilité, ainsi que l’explicite ce cher Ian Malcolm. Un système chaotique est un système qui présente une telle sensibilité aux conditions initiales que les infimes variations vont produire des résultats divergents.

Comme ces gouttes d’eau placées au même endroit de la main mais qui suivent des trajectoires très différentes même si les conditions initiales, elles, ont peu varié.

Fin de l’extrait de Jurassic Park

♪♪♪ Pause musicale : « It’s Oh So Quiet », Björk

Vous êtes bien sur Radio Campus, dans Artborescience, l’émission qui génère des turbulences tranquilles.

♪ Tapis : « Cache-cache », Jacques Burtin

Par cette observation inattendue, Edward Lorenz découvrit ce qui allait être à l’origine d’une nouvelle science. Une nouvelle science, mais qui trouve ses racines dans les mathématiques et la physique de la fin du XIXe siècle avec Henri Poincaré, et le problème à trois corps : pour voir apparaître le chaos, il suffit de faire graviter trois corps les uns autour des autres, ou de provoquer une collision simultanée entre trois corps. Les lois déterministes de Newton, qui permettent de prédire exactement les orbites de deux corps gravitant l’un autour de l’autre, ne permettent que des approximations successives pour les problèmes à trois corps ou plus. Cela tient à la nature des équations mathématiques en jeu. On ne parlait pas encore de chaos à l’époque – le terme n’existait pas encore dans l’acception qui nous intéresse. Mais on avait l’intuition de la nature de ces phénomènes. Pendant des décennies, ces problèmes ont été cachés sous le tapis.

Ils étaient gênants. Car l’imprévisibilité de ces systèmes semblait saper le déterminisme hérité de la physique de Newton. Le mathématicien Pierre Simon de Laplace se fit le chantre du déterminisme par cette célèbre prose : « Pour une intelligence qui embrasserait dans la même formule les mouvements des plus grands corps de l’univers comme ceux du plus léger atome, rien ne serait incertain pour elle, et l’avenir comme le passé serait présent à ses yeux. »

L’idée de ce déterminisme de Laplace est qu’il suffit de connaître parfaitement les conditions initiales d’un système pour pouvoir prédire exactement l’état de ce système à n’importe quel instant, futur ou passé. Or, pour les systèmes chaotiques, il n’en est rien ! Tout d’abord, nous ne pourrons jamais connaître avec une précision parfaite la position initiale d’une particule réelle : cela nécessiterait une puissance de calcul infinie. Surtout, l’imprévisibilité des systèmes chaotiques ne tient pas qu’à ces imprécisions. L’extrême sensibilité aux conditions initiales ne résulte pas que de notre connaissance partielle de ces conditions. Cette imprévisibilité est intrinsèque au système, divergente et croissante, comme si la nature balayait de ses ailes moqueuses et exubérantes de liberté la formule de Laplace.

Une théorie transversale – entropie – complexité – vie

Le chaos, au sens scientifique, n’est donc pas synonyme de désordre, bien que les phénomènes observés à l’origine de cette théorie aient, dans une acception courante, une apparence de désordre et d’irrégularité. En vérité, cette apparence trompeuse de désordre et d’irrégularité résulte de la complexité des phénomènes observés. Or, qui dit complexité, dit ordre.

La théorie du chaos apporte des éléments de réponses à ces questions : comment des îlots de complexité peuvent-il naître dans un monde voué à évoluer toujours vers un plus grand désordre ? Comment la vie apparaît-elle ?

Éclaircissons un point : pourquoi l’univers serait-il voué à évoluer vers un plus grand désordre ? C’est la fameuse seconde loi de la thermodynamique, celle de l’entropie. En physique, ce qui est synonyme de désordre, c’est l’entropie. Plus précisément, l’entropie est la mesure du désordre d’un système (ce qui manque encore d’exactitude, mais j’y reviens plus tard). Et la seconde loi de la thermodynamique – la thermodynamique qui est la branche de la physique qui étudie les échanges de chaleur et d’énergie – nous dit que l’entropie – c’est-à-dire le désordre – d’un système isolé, ne peut qu’augmenter ou rester constante avec le temps. C’est-à-dire que son énergie ne peut que se dissiper, se dégrader d’une manière irréversible.

Les Ruines de l’Eglise du Vieux Bourg – Le vieux Bourg 19220 SAINT GENIEZ O MERLE

Mais concrètement, qu’est-ce que ce désordre ? Quelle apparence prend cette entropie et en quoi consiste-t-elle ?

Revenons aux origines de la thermodynamique. Cette science est née au XIXe siècle tandis l’on cherchait à améliorer le rendement des machines thermiques. Le constat est qu’une machine ne peut pas avoir un rendement de 100%. Il y a toujours des pertes, une partie de l’énergie qui ne peut pas être utilisée.

Les corps chauds communiquent leur chaleur aux corps froids. Cette énergie thermique peut être utilisée ; transformée en énergie mécanique, par exemple. C’est le principe du moteur. À la fin du processus, tous les corps ont la même température : le système a atteint l’équilibre. Il n’y a alors plus d’énergie utilisable. Cette uniformisation, cet équilibre, fait croître l’entropie. L’entropie mesure le désordre d’un système et la dégradation de son énergie. Lorsqu’un système isolé est à l’équilibre, son entropie est maximale. Attention, ne négligeons pas un point : l’énergie d’un système isolé se conserve : c’est la première loi de la thermodynamique ; mais, c’est la qualité, la forme de l’énergie qui change. Et la deuxième loi nous dit que la qualité de l’énergie ne peut que se dégrader dans un système isolé.

Pour qu’il y ait du mouvement, pour qu’il y ait de la vie, de l’ordre, il faut du déséquilibre.

Ce que le scientifique considère comme étant de l’ordre, c’est la quantité d’informations nécessaire pour décrire un système, c’est son degré d’organisation. Plus un système est hétérogène, organisé, ordonné ; plus il contient d’informations, plus son entropie est faible. Plus un système est uniforme, homogène, plus son entropie est grande.

(note post émission, deux ans plus tard : réajustement de la notion d’entropie en fin d’article, en compagnie d’Aurélien Barrau)

♪ Tapis : « Firmament », OST du jeu GRIS

Prenons un exemple mécanique et sans échange de chaleur : une goutte d’encre plongeant dans un verre d’eau. Etat initial : une goutte d’encre d’un côté, et l’eau de l’autre côté. La goutte tombe dans l’eau. Nous voyons d’abord les volutes colorées de l’encre se déployer et onduler gracieusement dans le liquide transparent. Ces arabesques chaotiques se meuvent et s’estompent lentement en poursuivant leur danse.

L’état final observé : une encre entièrement diluée et un liquide homogène. Un retour spontané à l’état initial ne sera jamais possible. Alors non non, n’essayez pas d’invoquer l’incertitude quantique ou je ne sais quoi : à cette échelle, ça ne fonctionne pas… Pour des raisons statistiques, des lois statistiques qui prédisent le comportement d’un grand nombre de molécules plus ou moins agitées. Non, les pigments de votre encre ne vont pas spontanément tous se regrouper pour former la goutte initiale que vous avez laissé tomber. Ce n’est pas possible. Le phénomène est irréversible.

Tout système fermé est voué à voir son désordre croître, irréversiblement. L’entropie de l’Univers ne peut qu’augmenter… globalement. Car, localement, dans cette soupe qui évolue vers toujours plus d’entropie, flottent des croûtons qui, eux, évoluent vers toujours plus de complexité. Des crotons très ordonnés, dont nous, les humains, sommes de savoureux représentants. Les êtres vivants, pour rester vivants, doivent maintenir un déséquilibre avec leur environnement. Pour un être vivant, atteindre l’équilibre, c’est-à-dire l’entropie maximale, c’est la mort.

Le second principe de la thermodynamique est toujours respecté : un système non isolé, tel qu’un organisme vivant, peut augmenter sa complexité – c’est-à-dire diminuer son entropie – si en contrepartie l’entropie extérieure augmente davantage de telle manière que le bilan sera bien une augmentation globale de l’entropie. Augmenter sa complexité, cela implique de dégrader l’énergie environnante, et donc d’augmenter l’entropie de notre environnement. Ainsi que l’écrit Erwin Schrödinger dans son ouvrage Qu’est-ce que la vie : un organisme vivant se nourrit d’entropie négative. L’enjeu du métabolisme est de réussir à débarrasser l’organisme de toute l’entropie qu’il produit pour rester en vie. L’organisation est maintenue par une extraction d’ordre du milieu environnant.

♪♪♪ Pause musicale : « Pays Sauvage », Emily Loizeau

Vous êtes bien sur Radio Campus, dans Artborescience, l’émission qui gazouille et qui papillonne.

La complexité des organismes vivants se maintient grâce à une extraction d’ordre de leur milieu environnant.
Qu’appelle-t-on exactement complexité ?

♪ Tapis : L’orage, Jacques Burtin

Au sens courant, complexe s’oppose à simple : c’est ce qui contient beaucoup d’éléments différents. Cela rejoint l’idée d’ordre, de quantités d’informations, opposé au désordre de l’entropie. Plus c’est hétérogène, plus c’est ordonné, plus c’est complexe.

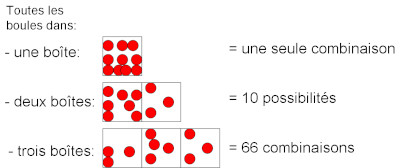
Image du site https://webinet.cafe-sciences.org/articles/au-fait-cest-quoi-lentropie/

Il n’y a pas de définition de la complexité unique et commune à toutes les disciplines scientifiques. La complexité est une mesure assez intuitive. Nous entendons souvent les scientifiques louer le cerveau humain comme étant la structure la plus complexe de l’univers. La vie, puis le psychisme qui en émerge, représentent des niveaux de complexité toujours supérieurs. Les organismes vivants sont des systèmes qui contiennent et qui traitent une quantité colossale d’informations. Ce sont des systèmes à très faible entropie.

Le physicien Robert Laughlin définit la complexité d’une forme par l’instabilité du processus physique qui l’a engendrée. C’est-à-dire qu’une forme est d’autant plus complexe qu’aurait été grande sa variété si les conditions de sa naissance avaient été très légèrement différentes. On rejoint la définition du chaos. Ainsi, pour Robert Laughlin, complexité égale ordre égale chaos.

Cette imprévisibilité des formes complexes est à relier à la notion de déséquilibre thermique. Les transformations menées à l’équilibre tout du long engendrent des formes prévisibles… Une eau qui refroidit très lentement – toujours à l’équilibre – produira un bloc de glace monotone. Du sel cristallisant dans l’eau très lentement produira un bloc de sel monotone. Tandis que si le refroidissement est rapide, l’eau gèlera en formant des cristaux tous différents, tous uniques. Le sel cristallisera en formant un enchevêtrement fin d’aiguilles. Les transformations survenant à l’état de déséquilibre engendrent la diversité, la variété, une forme de complexité.

Annick MONNIER — Travail personnel — Fleur de givre, à Lajoux, Jura, France

Une brève histoire de l’Univers : mort thermique de l’Univers et pyramide de la complexité

♪ tapis : Extrait de « Tristan et Isolde », Wagner

L’entropie de l’Univers ne peut qu’augmenter, en vertu de la seconde loi de la thermodynamique. Cela a conduit des scientifiques, au XIXe siècle, à envisager la mort thermique de l’Univers : un état isotherme où plus aucune énergie ne serait utilisable, un Univers à entropie maximale où tout mouvement serait devenu impossible… Un Univers mort et statique.

Peut-on vraiment assimiler l’évolution de l’Univers à une sorte d’inévitable Ragnarok des étoiles ? Et si l’Univers est voué à évoluer toujours vers un plus grand désordre, cela signifie-t-il que l’Univers part d’un ordre primordial pour, en quelque sorte, dégénérer ensuite ?

Cette idée dominait au XIXe siècle, mais la cosmologie du XXe siècle nous apprend qu’au contraire, la soupe thermique est derrière nous. Une soupe thermique est peut-être devant nous – c’est une hypothèse ; mais en tout cas, il y a une soupe derrière, à l’origine : l’Univers semblerait plutôt partir d’un chaos primordial – chaos au sens courant, cette fois-ci. Comme dans la Théogonie d’Hésiode : « Chaos, gouffre primordial à l’origine de toutes choses ». « Ce sauvage abîme, écrit Milton dans Le Paradis perdu, ce sauvage abîme berceau de la nature, et peut-être son tombeau. »

Image de ruines générée avec Midjourney. C’est méta.

La mise en évidence de l’expansion de l’Univers avant le milieu du XXe siècle a conduit à élaborer le modèle cosmologique du Big Bang. Ce modèle décrit un Univers qui aurait été plus chaud et plus dense par le passé, et qui aurait consisté, dans l’un de ses jeunes instants, en une soupe primordiale de particules.

De ce chaos primordial, depuis cette soupe, l’Univers évolue vers toujours plus d’ordre. L’Univers-soupe était plus homogène qu’aujourd’hui, donc moins ordonné. Depuis la naissance de notre Univers, la matière gravit les échelons de la complexité. Les grandes divinités organisatrices de ce désordre primordial portent les noms d’interaction nucléaire forte, de force électromagnétique, et de gravité.

L’interaction nucléaire permet l’édification des atomes. La force électromagnétique lie les atomes pour dessiner les molécules. La force de gravité façonne les étoiles, engendrant ainsi les écarts thermiques qui permettent l’apparition de phénomènes chaotiques et l’émergence de structures toujours plus complexes, tout en augmentant l’entropie globale.

Cela semble contradictoire… Et ça l’est, en effet. Je vous propose quelques pistes de compréhension à la fin.

Une multitude de scénarios est envisagée pour décrire la fin de notre Univers. Ces scénarios diffèrent les uns des autres en raison de l’incertitude sur la valeur de la constance cosmologique, sur l’énergie sombre, ou encore sur la durée de vie du proton… Sera-ce un Big Crunch avec une sorte de retour à l’état initial : une soupe de particules élémentaires, puis un espace-temps désagrégé en mousse quantique ? Ou bien l’univers terminera-t-il en un grand bain froid, en une soupe de particules infiniment diluée  ? Ou bien encore sera-ce un grand déchirement, un Big Rip, laissant un Univers sans plus aucune structure ?

Pour chacun de ces scénarios, il est possible d’imaginer quelles stratégies la vie, l’intelligence, la conscience, l’esprit pourront mettre en œuvre pour se perpétuer le plus longtemps possible.

Production personnelle

Tentons de résumer :

L’histoire de l’Univers – du moins celle que nous connaissons – est celle de l’édification de structures toujours de plus en plus complexes. Les êtres vivants semblent être au sommet de la pyramide de la complexité.

L’Univers-soupe du début a formé des grumeaux grâce à la force de gravité : la gravitation est en quelque sorte une réductrice d’entropie. Ces grumeaux que sont les étoiles provoquent les écarts thermiques qui permettent l’existence de systèmes ouverts très éloignés de l’équilibre thermique au sein desquels la complexité peut apparaître.

Ces systèmes complexes, ces systèmes ordonnés, sont caractérisés par leur imprévisibilité, qui donne une impression de désordre, au sens courant.

Cela dit, les systèmes chaotiques ne présentent pas forcément tous une structure très complexe, pas forcément aussi complexe que celles des êtres vivants. Nous l’avons dit : le chaos commence à apparaître dans le problème à trois corps, par exemple… Finalement, le chaos apparaît dès lors qu’un système influence son propre comportement. Cette rétroaction engendre la complexité du comportement du système.

Ainsi, un système apparemment simple peut présenter des comportements complexes, et ainsi la matière gravit les échelons de la complexité, en structurant un Univers pourtant voué à l’entropie.

♪♪♪ Pause musicale : « Poussières », Merzhin

Vous êtes bien sur Radio Campus, dans Artborescience, l’émission qui se nourrit d’entropie négative.

♪ Tapis : « Ys », album « Renaissance de la harpe celtique », de Alan Stivell

Les formes fractales

La beauté de la vie et sa diversité procèdent du chaos qui les caractérise. Cette beauté, cette diversité, nous les retrouvons dans les formes fractales propres aux systèmes chaotiques.

Notre cher météorologue, Edward Lorenz, en étudiant les mouvements chaotiques de convection de l’air, découvrit que le point représentant le système météorologique décrivait dans l’espace de Poincaré (Henri Poincaré qui fut d’ailleurs le pionnier de la théorie du chaos au tout début du XXe siècle) – Edward Lorenz découvrit que ce point traçait une figure folle et enchevêtrée, dessinant deux boucles comme les ailes d’un papillon de Moebius. Cette figure, qu’on appelle attracteur, est dit étrange car on ne peut prévoir dans quelle boucle le point se situera dans l’instant suivant.

Lorenz observa aussi que les boucles de son attracteur, serrées à l’infini, répétaient le même motif mais à des échelles différentes. L’attracteur étrange contient de la régularité dans ce qui semblait être irrégulier ; de la régularité dans une succession infinie d’échelles : il s’agit d’un objet fractal. Une manifestation visuelle de l’ordre du chaos.

Benoît Mandelbrot, employé chez IBM dans les années 60, découvrit lui aussi des fractales dans un domaine tout différent ; l’économie. Les fluctuations apparemment aléatoires du cours du coton se composaient de hautes fluctuations qui subissaient l’influence des plus courtes, et se décomposaient en variations à court et à long terme tout-à-fait différentes. Mandelbrot entreprit de dresser une peinture géométrique de ces fluctuations, avec l’intuition que la symétrie qu’elle contenait se révélait à différentes échelles.

Cette symétrie d’échelle est ce qui caractérise les figures fractales.

Mandelbrot avait trouvé la véritable géométrie de la nature. C’est avéré : la Nature aime les fractales. La formation des cristaux, la croissance des végétaux, le réseau sanguin et les galaxies présentent une géométrie fractale. Le chou romanesco est l’un des objets naturels les plus remarquables à ce propos.

Si l’on entreprend de mesurer la longueur de la côte bretonne, qui présente un caractère fractal, avec une précision de plus en plus fine, elle tendra vers l’infini : les segments décrits par des anfractuosités de plus en plus petites sont de plus en plus nombreux. Un tel objet échappe à la géométrie euclidienne. Une longueur infinie est contenue dans une surface finie. Afin de mesurer le degré de rugosité, le degré de fragmentation de ces formes, Benoît Mandelbrot introduisit des dimensions fractionnaires. Une ligne fractalement brisée présentera une dimension supérieure à 1, mais inférieure à 2 : entre la ligne et la surface.

Ce terme de fractales, nous le devons à Mandelbrot. Il cherchait un nom pour désigner ces formes à dimensions fractionnaires en feuilletant au hasard son dictionnaire de latin. Il tomba sur l’adjectif fractus, signifiant brisé.

Zoom sur l’ensemble de Mandelbrot

Chaos, figures fractales et arts visuels

Les mouvements spontanés du peintre américain Jackson Pollock évoquent le chaos au sens courant : le désordre. Il émerge cependant de ces giclures, de ces éclaboussures, ce charme authentique des formes naturelles et complexes, ce qui nous amène au chaos, au sens de la théorie du chaos cette fois-ci. Les œuvres de Jackson Pollock ne donneraient-elles pas d’ailleurs une vraie impression fractale ? Dans un article paru dans la revue Nature du 3 juin 1999, Fractal Analysis of Pollock’s drip paintings, des physiciens relèvent que le dripping de Pollock présente une dimension fractale qui s’accroît tout au long de sa carrière.

Feel Good Fractals: From Ocean Waves to Jackson Pollock’s Art

À l’opposé de l’apparence des œuvres de Jackson Pollock, quoi de plus précis, de plus ordonné que les mosaïques islamiques ? Des motifs similaires, des étoiles et des entrelacs, se répètent et s’imbriquent à différentes échelles, comme une préfiguration de l’art fractal. Il en va de même de la calligraphie enchevêtrée du Livre de Kells, de ses entrelacs et de ses spirales emboîtées, qui nous aspirent, tourbillonnent puis nous font rebondir d’une sphère à l’autre, plus grande ou plus petite.

Références pour les motifs islamiques :
tombe de Hafez, à Shiraz (Iran)
Sultanhani caravanseray ( Aksaray/Turkey , encadrement de porte – photo de Wolfgang Saube
manuscrit enluminé du début du XVIIIe siècle

L’encre et l’aquarelle se prêtent bien à l’apprivoisement du chaos. Les formes chaotiques dues au jeu de diffusion des pigments dans les anfractuosités du papier donne aux êtres ou aux choses peintes la beauté de la spontanéité. L’art du lavis résulte d’un équilibre entre contrôle des formes et lâcher-prise – laisser faire son travail au chaos pour que ces formes donnent l’impression de s’être dessinées toutes seules. La maîtrise résulte de cet équilibre. Et même dans l’hypothèse d’un contrôle total, c’est souvent l’illusion de la spontanéité qui rend les formes gracieuses.

Zhu Da, ou Bada Shanren, fut un peintre chinois du XVIIe siècle. Ses coups de pinceau vifs et spontanés lui ont valu le surnom de peintre sauvage. L’aspect fascinant de ses lavis tient à la sensation que ses arbres, ses roches, ses oiseaux et ses poissons ont émergé spontanément des taches d’encre. Dans l’immense variété de son œuvre prolifique, Hokusai nous offre de nombreuses occasions de nous émerveiller de la sorte. Son jeune coq, peint vers 1825, se compose d’une grande tache d’encre noire dégradée, agrémentée simplement de lignes cette fois-ci très fines et très précises pour le bec, les yeux, les pattes. Le corps de ce coq semble s’être étiré de lui-même sur le papier. Point de fractals ici, mais des formes élégantes et gracieuses, comme les volutes chaotiques de la fumée.

Oiseaux par Bada Shanren

Dans les années 80 et à mesure que la puissance des ordinateurs grimpait, l’art numérique fractal s’est développé, en 2D puis en 3D. À partir d’une simple formule itérée, se déploient des formes toujours similaires mais toujours légèrement différentes, apparaissant à l’infini en zoomant toujours plus. L’ensemble de Mandelbrot rassemble des points obtenus par l’itération d‟une même opération, et forment ainsi l’une des figures fractales les plus célèbres. Chaque particule en révèle une multitude, et chaque particule, bien qu’étant semblable à l‟île centrale, en est légèrement différente.

James Gleick, dans son ouvrage La Théorie du chaos, fait ainsi le portrait de cette peinture mathématique homéomérique : « Chaque nouvelle molécule serait entourée de ses propres spirales et de ses propres projections en forme de flammes, qui, à leur tour, révèleraient des molécules encore plus minuscules, toujours semblables, jamais identiques, […] miracle de miniaturisation dans lequel chaque détail devait inévitablement être un univers en soi, différent et complet. »

Autre zoom sur l’ensemble de Mandelbrot

Ces îlots, naissant les uns des autres, nous font penser à ces îlots de complexité qui émergent les uns des autres en présentant à chaque fois une originalité, permettant une nouvelle expérience… Ces ilots que sont les organismes vivants. Nous sommes des îlots de complexité nés du chaos, comme si le chaos exprimait la créativité de l’Univers.

Si le chaos est vecteur de beauté, il semble être vecteur de liberté. Nous affranchit-il de notre propre déterminisme ? Est-ce en lui que pourrait résider notre propre part de créativité et notre libre arbitre ? Comme si nous étions les compositeurs et interprètes de nos propres vies.

Comme des musiciens de jazz.

♪ Tapis : « MISTERIOSO », New Monk Trio, Laurent De Wilde

Le physicien Trinh Xuan Thuan estime qu’ « au lieu d’être déterminé à l’avance comme une partition de musique classique, le destin de l’univers est ouvert. La nature joue en quelque sorte du jazz. Comme le jazzman improvise autour d’un thème général pour créer des sons nouveaux, elle brode sur les lois intemporelles de la physique pour générer la beauté et la complexité du monde. »

Selon la Révérende Mère Darwi Odrade, personnage marquant de la saga Dune de Frank Herbert, le jazz parle en faveur de la vie. Jamais deux interprétations exactement semblables. Chaque musicien réagit à ce qu’il reçoit des autres. Cette auto-référence, cette auto-organisation, caractérise les systèmes chaotiques. Lorsque la Révérende Mère appréhende la confrontation finale avec les Honorées Matriarches, elle estime que cette bataille devra être jouée d’oreille. Les plans, les analyses préalables ont leur limite, bien que l’ennemi puisse être analysé sans fin… Ce n’est pas une analyse sans fin qui assurera la victoire, mais la combinaison d’une analyse consciente de ses limites et de la capacité à sentir l’instant, à le saisir et à improviser.

Charlie Parker (saxophone), Tommy Potter (contrebasse), Miles Davis (trompette), Duke Jordan (piano) et Max Roach (batterie, à peine visible sur la photo) en concert à New York, en 1947

« Il n’y a pas de secret à l’équilibre, nous dit la Révérende Mère : il suffit de sentir les vagues. » Les vagues fractales, les petites vagues sur les moyennes vagues sur les grandes vagues, comme celle d’Hokusai ; les petites vagues qui s’unissent pour former les moyennes et les grandes, pour former des rouleaux à surfer, ou des tsunamis à fuir.
Cette imprévisibilité, ce chaos, tirons en parti dans l’amor fati ; l’amour de la destinée prôné par Marc Aurèle. Émerveillons-nous de toutes ces beautés, même des plus déroutantes. Saisissons ces surprises du chaos pour exprimer notre puissance, notre propre créativité, notre capacité de transformation, dans cet équilibre entre lâcher-prise et contrôle. Surfons avec joie sur les vagues chaotiques de notre destin.

La Grande Vague de Kanagawa, Hokusai

L’émission touche presque à sa fin. Merci au professeur Sattler et docteur Malcolm pour leur intervention.

Petit extrait – re extrait Jurassic Parc

Juste avant les références, bonus de l’article : l’entropie expliquée par Aurélien Barrau

Lors d’une conférence exposant une approche cosmologiste du temps, Aurélien Barrau évoque le problème de l’entropie initiale de l’Univers et une hypothèse sur la nature de l’entropie :
https://www.youtube.com/watch?v=6GFzP8u7sDg
à partir de 42 minutes environ

Transcription du passage :

« Mais ce que je vais dire à partir de maintenant – je commence à rentrer, là, pour mon dernier quart d’heure, dans la science spéculative. Donc là, je m’aventure sur des choses qui ne sont pas corroborées par l’expérience, et qui sont donc à prendre avec des pincettes : je vous parle de recherches en cours. Donc, cette gravité quantique pourrait nous conduire à penser que quand on remonte dans le passé – très très proche du Big Bang – vint un instant (si l’on peut dire) où le temps disparaît. C’est-à-dire que initialement (évidemment, le mot « initialement » est à mettre entre une infinité de guillemets), l’Univers serait dans un état purement spatial, avec quatre dimension d’espace, et en réalité le temps semblerait émerger d’une sorte de transition de phase, un peu comme de l’eau qui gèle. Au départ, dans l’eau, les molécules sont dans tous les sens. Puis quand elles se mettent à geler, paf, toutes les molécules s’alignent. C’est ce qu’on appelle une transition de phase. Eh bien, il y aurait une forme de condensation, peut-être, de l’état cosmologique qui induirait l’émergence d’une dimension de temps, mais qui pourrait être éventuellement différente en différents lieux. On pourrait imaginer, finalement, que le sens du temps ne serait pas exactement le même à l’échelle d’une superstructure cosmique.

Et le dernier problème que je voudrais évoquer – qui est le plus important, je pense, par rapport à ce qui nous intéresse aujourd’hui –, c’est le problème de l’entropie initiale de l’Univers. Et ça, c’est fondamental à la fois du point de vue de la compréhension de l’Univers, du temps et de la vie. Vous savez peut-être que l’une des lois fondamentales de la physique, qu’on appelle la deuxième loi de la thermodynamique, c’est le fait que l’entropie augmente, sous certaines conditions que… je décris pas… L’entropie, c’est à la fois une mesure du désordre d’un système et une mesure de l’information qui nous manque sur ce système. C’est essentiellement la même chose, et c’est facile de s’en convaincre : si vous avez plein de flèches ordonnées, qui sont toutes parallèles, alors c’est très ordonné parce que si vous connaissez l’état d’une seule, alors vous connaissez l’état de toutes les autres. Au contraire, si le système est complètement désordonné : les flèches sont parfois en haut, parfois en bas… Si c’est complètement désordonné, en en voyant une seule, vous n’en connaissez qu’une seule. Donc, vous voyez bien que plus c’est désordonné, plus il vous manque d’informations… à partir d’une visions parcellaire. Ce qui est important, c’est que cette entropie va toujours augmenter spontanément dans l’évolution des systèmes [fermés]. Alors ça, c’est vraiment important de comprendre que ce n’est pas une espèce de loi mystérieuse ou mystique qui aurait un goût prononcé pour le désordre. Qu’est-ce qu’il se passe ? Pourquoi la goutte de lait diffuse dans le café et donc évolue d’un état ordonné – le lait est condensé – vers un état désordonné, où le lait est diffusé dans le café ? C’est pas parce que les molécules sont « attirées », c’est uniquement parce que c’est plus probable d’être désordonné qu’ordonné. […]

Et donc l’augmentation du désordre, de l’entropie etc. c’est juste l’évolution spontanée des systèmes vers les configurations les plus probables. Et ça marche très bien, et c’est une des lois les plus fondamentales de la science, et probablement les plus fiables. Mais alors, ça pose une question, ça : c’est qu’actuellement, l’entropie […] de l’Univers actuel est assez faible, en fait. Par rapport à sa valeur maximale théorique, on est très loin. Pourtant, l’entropie n’a fait qu’augmenter depuis 13 milliards d’années. Donc, ça veut dire que l’entropie initiale de l’Univers était extraordinairement faible. Donc, ça veut dire que ça correspondait à un état extraordinairement improbable. Alors ça, c’est bizarre. C’est bizarre parce que… pourquoi est-ce qu’un état au hasard (a priori) de l’univers est justement un état qui est incroyablement improbable ? ça, ça contredit complètement les corroborations scientifiques… Quand vous avez un échantillon au hasard, s’il est très improbable du point de vue de votre théorie, c’est généralement que votre théorie ne marche pas. Or, cette théorie de l’entropie, on est à peu près sûrs qu’elle marche parce que c’est peut-être la plus utilisée de toute la physique.

Et vous avez déjà compris qu’il y a évidemment un lien entre l’entropie et le temps… Parce que, qu’est-ce qui fait qu’on voit le temps passer ? C’est précisément que l’entropie augmente. Quand je lance une balle de tennis comme ça, elle fait une parabole… Si on passe le film à l’envers, elle fait une parabole dans l’autre sens… C’est impossible de savoir quand le film est à l’endroit ou à l’envers, parce que c’est un système simple. Il n’y a pas de création d’entropie, pas de création de désordre. Le film à l’endroit, le film à l’envers, c’est les mêmes. Alors que la goutte de lait dans le café qui diffuse, là je sais que quand le film est à l’endroit : c’est quand elle diffuse, et quand le film est à l’envers, c’est quand elle se recondense. Là, c’est pas invariant par renversement du temps. Pourquoi c’est pas invariant ? Parce qu’on crée de l’entropie. Donc, vous voyez que l’orientation du temps – le fait qu’on vieillisse, quoi – c’est fondamentalement lié à l’augmentation de l’entropie. Et l’augmentation de l’entropie, elle nous dit que l’Univers doit être dans un état initial qui est hautement improbable. Et ça, c’est un grand paradoxe. C’est une des questions les plus fondamentales de la physique, qui est connue depuis au moins un siècle. Alors, il y a des explications très savantes et très techniques, mais je voudrais mentionner une explication très intuitive, et que je trouve extrêmement convaincante et extrêmement belle, de mon ami le physicien Carlo Rovelli qui est un grand spécialiste de gravité quantique. Alors, je fais la version ultra simplifiée de l’argument, mais ça a été publié de façon bien plus technique que ça… Et donc, l’idée, qui est très liée à la définition du temps, c’est la suivante : oui mais en fait, c’est pas vrai que l’entropie d’un système augmente spontanément ! Ce qui va définir l’augmentation de l’entropie – l’augmentation du désordre – c’est pas quelque chose d’objectif, en fait. C’est une manière particulière de regarder le système. Je vais essayer de donner un exemple extrêmement simple. Vous avez une boîte, avec une paroi… Là, vous avez des p’tites billes rouges, et là des billes bleues… Puis les billes peuvent être soit circulaires, soit cubiques, soit ellipsoïdales… Donc plusieurs formes différentes. Et vous mettez toutes les rouges ici, et toutes les bleues ici. Et puis, vous regardez que la couleur. Vous enlevez la cloison, vous remuez la boîte… Qu’est-ce que vous allez dire ? Ah bah ça évolue vers le désordre. Au départ, c’était ordonné : j’avais les rouges d’un côté, les bleus de l’autre… J’ai remué, maintenant j’ai à peu près autant de rouges et de bleues des deux côtés… Normal : l’entropie du système a augmenté.

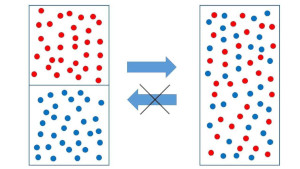
Mais si au lieu de regarder la couleur des billes, vous regardez leur forme. Je l’ai dit au départ : les formes, elles étaient déjà au hasard. Quand vous avez agité la boîte, l’entropie n’a pas du tout augmenté. Vous étiez désordonné, vous êtes toujours désordonné. Question : la vraie entropie, elle a vraiment augmenté ou pas. Réponse ? Y a pas de réponse. Ça dépend de la chose qui est importante pour vous. Du point de vue de la couleur, elle a augmenté. Du point de vue de la forme, elle est restée constante. Quelque part, avec mille guillemets, le temps s’est écoulé pour les gens qui sont sensibles à la couleur. Le temps ne s’est pas écoulé pour les gens qui sont sensibles à la forme. L’hypothèse de Rovelli, de ce point de vue-là, ce n’est pas en fait que l’état initial de l’Univers était particulier avec un désordre ou une entropie très basse. C’est simplement que nous, en tant que systèmes vivants, on se couple au reste de l’Univers d’une manière qui maximise la production d’entropie. Pourquoi ? Parce que c’est ça, être vivant. Être vivant, que ce soit du point de vue cellulaire, avec l’ADN, ou du point de vue psychologique avec la mémoire… Être vivant, c’est avoir un rapport au passé, c’est avoir une histoire. Nous sommes nos histoires. Psychologiquement et physiquement, nous sommes notre passé. Un système physique qui ne voit pas le temps existe, mais lui, il a un couplage avec l’Univers qui fait qu’il ne peut pas être vivant. Ce qui fait que nous sommes des systèmes vivants, c’est précisément que nous nous couplons – c’est-à-dire que nous avons des interactions avec le reste de l’Univers qui fait que nous voyons un univers pour lequel le temps passe. Donc, le passage du temps c’est – c’est ce que je vous disais – à la fois une définition du vivant et du temps. Le passage du temps, dans cette acception-là, c’est pas quel que chose d’a priori… C’est quelque chose d’a posteriori qui est apparent pour certains types d’interactions avec le monde qui nous entoure. Les systèmes qui interagissent avec le monde qui les entoure de manière à maximiser les variables qui font émerger une augmentation du désordre sont des systèmes qui ont toute les chances de développer des capacités de complexité qui sont celles du vivant. Donc, je pourrais donner beaucoup d’exemples en ce sens, mais c’est l’idée globale. Alors, c’est très débattu ! Je finis le dernier quart d’heure sur de la science en train de se faire… Mais quelque part, vous voyez, en même temps, l’immensité de notre inconnaissance, parce qu’on en est encore à se poser des questions aussi géniales et aussi naïves que celles-là, finalement… Et donc, ça montre que la question de la nature fondamentale du temps en physique théorique est loin d’être résolue. Évidemment, je pense que ça appelle des questions de nature philosophique, dans une vision post-kantienne, c’est-à-dire un temps qui n’est plus transcendantal mais qui serait au contraire a posteriori – donc peut-être une vision, je ne sais pas, goodmanienne et derridienne de ce que pourrait être la dimension temporelle. Tout pratiquement reste à écrire de ce point de vue. »

Aurélien Barrau complète l’explication en répondant à une question du public :

Question : «  Cette notion que l’entropie (et donc quelque par le passage du temps ou l’irréversibilité du temps, la probabilité d’un état etc.) était liée à l’existence d’organismes vivants… Je ne sais plus exactement comment vous m’avez formulé… Du coup, ça donne l’impression qu’avant que la vie apparaisse, le temps était différent ou est-ce que… Comment est-ce qu’on peut voir ça ?

Réponse : « ¨Peut-être j’ai pas été clair, mais vous avez raison, c’est pas dans ce sens là qu’il faut le dire bien sûr, parce que là ça reviendrait à cette téléologie… c’est comme s’il fallait que la vie existe et pour que le temps existe, ce qui n’est pas du tout – au contraire même – ce qui est absolument pas l’idée de cet argument.

Non, disons que cet argument, il consiste à dire, par exemple… Prenons la Terre, parce que c’est un système qu’on connaît tous… Essentiellement, la Terre reçoit l’énergie du soleil, donc de la lumière qui arrive avec une certaine énergie E, un certaine fréquence µ… Et puis la Terre re-rayonne de l’énergie – exactement la même quantité d’énergie puisqu’on est à l’équilibre – avec une fréquence différente un peu plus petite. E le fait que la fréquence soit un peu plus petite, ça veut dire que pour rayonner la même quantité d’énergie faut émettre plus de photons… Et donc, l’entropie est plus grande.

Et donc voilà, on a créé de l’entropie et évidemment, pour nous êtres humains, on a une source d’entropie négative gigantesque à disposition et c’est extraordinairement utile. Mais cette augmentation d’entropie n’est absolument pas liée à une solution particulière des équations de Maxwell. Si on regarde la solution de l’équation de Maxwell, elle ne dit rien sur la production d’entropie. Elle est liée au fait qu’il y a des choses – qui en l’occurrence sont les êtres vivants – qui utilisent de façon extrêmement utile ces deux choses qui sont l’énergie et la fréquence. Et parce qu’on se couple au monde extérieur en bénéficiant de la grandeur énergie et de la grandeur fréquence – parce que la grandeur fréquence elle est fondamentale pour pour beaucoup d’interactions, pour la manière dont on est nous mêmes nourris par l’énergie extérieure – alors en effet il y a une augmentation objective d’entropie. Dire que c’est pas une construction sociale : l’entropie augmente objectivement dès lors que j’ai choisi les variables macroscopique avec lesquels je me couple au système considéré. Alors comme vous êtes physicien je fais une réponse un tout petit peu plus technique, donc ce sera les trois secondes chiantes pour les autres…
En fait, c’est lié aux ???????????. Tout est là. C’est qu’il n’y a une définition de l’entropie que dès lors que j’ai un moyen-âge, et dans la manière dont je fais un ?????????? du système fondamental. C’est un théorème de Boltzmann, d’ailleurs… On peut toujours trouver en ?????????? tels que l’entropie soit croissance ou décroissance. Et donc, l’hypothèse est de dire : l’augmentation d’entropie, ce n’est pas une propriété des systèmes, c’est une propriété émergente qui vient d’un certain type de couplage entre les systèmes. Et les systèmes qui se couple de façon que la production d’entropie soit maximum, ce sont les systèmes vivants. Mais ça ne signifie pas, évidemment, qu’il n’y avait pas d’évolution dans l’univers avant la vie. Mon propos n’était absolument pas une espèce de psychologisation de l’existence du monde. »

Et l’émergence, c’est justement le thème des épisodes suivants !

Maintenant, c’est l’heure des références !

Voici six ouvrages qui ont été primordiaux dans la conception de cette émission et qui vous permettrons d’approfondir notre sujet, sujet que je n’ai évidemment fait que survoler et condenser à l’extrême durant les minutes que nous avons passées ensemble  :

• La théorie du chaos, vers une nouvelle science, de James Gleick, édité chez Flammarion – un ouvrage de référence qui vous éclairera sur les origines de la théorie du chaos et sur ses implications.
• Le chaos et l’harmonie, de Trinh Xuan Thuan, édité chez folio essais – qui retrace avec exhaustivité les étapes de l’édification de la complexité depuis la naissance de notre univers.
• Un Univers différent, de Robert Laughlin, édité chez Fayard – essai portant sur la théorie de l’émergence, intimement liée à la théorie du chaos
• Qu’est-ce que la vie, d’Erwin Schödinger, aux éditions seuil, ouvrage dans lequel le célèbre physicien se demandait comment la physique et la chimie pouvaient rendre compte des processus à l’œuvre dans un organisme vivant, et où il exprimait l’intuition de l’existence d’un cristal apériodique porteur de l’information génétique, à l’époque où l’ADN n’avait pas encore été découvert.
• L’heure de s’enivrer — L’univers a-t-il sens ? – d’Hubert Reeves, aux éditions seuil. Les notions centrales de cet essai-là sont la complexité et l’entropie : lorsque l’auteur y parle de chaos, c’est au sens courant, c’est-à-dire synonyme de désordre, et donc pas du tout au sens scientifique que nous avons tenté d’éclairer un peu aujourd’hui. Il n’est pas question de théorie du chaos dans ce livre, mais il est intéressant pour l’entropie et l’idée d’accroissement de la complexité.
• Le destin de l’Univers, de Jean-Pierre Luminet, qui tourne autour des trous noirs et nous propulse vers différents scénarios de fin de l’Univers.
• Ensuite, un livre que j’ai découvert après la rédaction du texte de cette émission : Simplicité profonde, de John Gribbin, aux éditions Flammarion. Le sous-titre en est : le chaos, la complexité et l’émergence de la vie – il répond donc parfaitement à la double problématique posée en début d’émission. Ce livre présente un angle d’attaque assez différent de celui que j’ai choisi : l’auteur met l’accent sur la simplicité des règles qui permettent l’émergence de la complexité. Il évoque la façon dont les structures complexes émergent au bord du chaos, avec une approche moins simpliste que la mienne, m’étant contenté, moi, d’affirmer, en gros : ordre = chaos. Lors de la prochaine émission, nous affinerons cette approche pour aborder la théorie de l’émergence.

Des générateurs de fractales, on en trouve pléthore, gratuitement. Pour ma part, je me suis amusée avec Chaos Pro il y a quelques années, pour générer des ensembles de Mandelbrot de toutes les couleurs.

Rubrique JV et référence capillotractée : Hatoful Boyfriend un jeu de drague de la mangaka Moa Hato, que vous pouvez télécharger sur Steam. Je m’étais dit, pour illustrer le chaos, quoi de mieux qu’un jeu dans lequel vos choix amoureux révèlent des vérités très inattendues. Des choix amoureux qui d’ailleurs en l’occurrence se portent tous sur des pigeons… Alors pas des hommes crédules, hein, mais des vrais pigeons, des volatiles.

Sur cette note ornithologique, je vous salue. Je vous retrouverai le mois prochain pour une nouvelle Artborescience dans laquelle nous continuerons de côtoyer le chaos afin d’aborder la théorie de l’émergence.

Synthèse des références :

Pauses musicales :

• It’s Oh So Quiet, Bjork
• Pays Sauvage, Emily Loizeau
• Poussières, Merzhin

Tapis musicaux (dans l’ordre chronologique) :

• Générique : If the Stars were mine, Melody Gardot
• UMN Mode, OST du jeu Xenosaga
• Cache-Cache, Jacques Burtin
• Firmament, OST du jeu GRIS
• L’orage, Jacques Burtin
• Extrait de Tristan et Isolde, Wagner
• Ys, album « Renaissance de la harpe celtique » de Alan Stivell
• MISTERIOSO, New Monk Trio, Laurent De Wilde

Références bibliographiques :

• La théorie du Chaos, vers une nouvelle science de James Gleick, édité chez Flammation
• Le chaos et l’harmonie, de Trinh Xuan Thuan, édité chez Folio
• Un Univers différent, de Robert Laughlin, édité chez Fayard
• Qu’est-ce que la vie ?, d’Erwin Schrödinger, chez Seuil
• L’heure de s’enivrer – L’Univers a-t-il un sens ? d’Hubert Reeves, chez Seuil
• Le destin de l’Univers, Jean-Pierre Luminet, chez Folio
• Simplicité profonde de John Gribbin, chez Flammarion

Quelques références pop culturelles évoquées plus ou moins légèrement :

• Jurassic Park de Steven Spielberg
• Jackson Pollock
• Bada Shanren, le peintre sauvage
• Hokusai, jeune coq
• Le livre de Kells
• Dune, Frank Herbert
• Hatoful Boryfriend, Moa Hato